Продолжаем тему анализа прибыли математическими методами. Как и в старые добрые времена, экономика интересует многих, в том числе математиков. Формальные методы ограниченны, но могут быть полезны практикам. В этой статье до практики далеко, но кто знает… Проблема построения кривой спроса и ее использования стара, как современная экономическая теория. Условная дата рождения этой проблемы – знаменитая работа А. Маршала (1890 г.). В чем причина ограниченности математического анализа? В изменчивости спроса, в отсутствие связи между затратами и ценой на многих рынках. Но там, где этого нет, методы авторов данной статьи вполне могут быть применены. А строгость изложения поможет практикам приспособить математические результаты к своей области.
Андрей Мицкевич, к.э.н., доцент Высшей школы финансового менеджмента АНХ при Правительстве РФ
Суть концепции управления стоимостью заключается в обеспечении роста рыночной стоимости бизнеса за счет определения ключевых факторов стоимости и воздействия на них.
Необходимо понимать, что стоимость, являясь стратегической целью бизнеса, создается не только стратегическими решениями, но и на оперативном и тактическом уровнях управления. Процесс принятия управленческих решений должен быть сфокусирован на факторах стоимости, имеющих количественное выражение. Эффективность управленческих решений на каждом уровне оценивается системой показателей, один из которых – прибыль.
Для эффективного управления на тактическом уровне, критерием которого выбрана прибыль, воспользуемся подходом, лежащим в основе концепции управления стоимостью. Прибыль зависит от факторов, степень влияния которых можно оценить с помощью коэффициентов эластичности ЕФ. Они показывают, на сколько процентов изменится прибыль при увеличении значения фактора на 1%.
Факторный анализ прибыли
Представим прибыль в виде функции:
![]() (1)
(1)
где Фi – i-й фактор прибыли. Принятие управленческих решений основано на анализе коэффициентов эластичности прибыли ЕФ к составляющим ее факторам. Относительное изменение прибыли выражается через относительные изменения факторов с помощью коэффициентов эластичности:
![]()
При традиционном факторном анализе [1] факторы считаются независимыми друг от друга, а коэффициенты эластичности вычисляются так:
![]() (2)
(2)
Однако управленческие мероприятия по воздействию на один из факторов должны проводиться с учетом возможных последствий, которые могут отразиться на других факторах. Для этого предлагаем уточненный факторный анализ прибыли, учитывающий взаимное влияние факторов [2]. В этом случае модель прибыли вместо зависимости (1) примет вид:
![]() (3)
(3)
Оценивать чувствительность прибыли к составляющим ее факторам в рамках уточненного факторного анализа будем с помощью уточненных коэффициентов эластичности ЕФ. Продифференцировав функцию, стоящую справа в (3) как сложную по фактору Фj, получим уточненный коэффициент эластичности прибыли к рассматриваемому фактору:
![]() (4)
(4)
Влияние факторов друг на друга представляет собой корреляционную связь, так как между их изменениями нет полного соответствия, а воздействие одних факторов на другие проявляется только в среднем при массовом наблюдении фактических данных. Для такой зависимости можно установить лишь тенденцию изменения результирующего фактора при изменении величины влияющего фактора. Корреляционная зависимость устанавливается на основании выборки из генеральной совокупности данных. Для данной тенденции можно установить теоретическую линию регрессии (рис.1), указывающую основное направление. Вокруг этой линии группируются точки корреляционного поля. Для характеристики связей экономических показателей можно воспользоваться, например, линейной зависимостью вида Фi = kФj + b. Здесь k, b – неизвестные параметры уравнения регрессии. Тогда искомая производная будет равна коэффициенту регрессии:
![]() (5)
(5)

Расчет коэффициента регрессии проводится на основании данных компании. Строится таблица соответствия (табл.1), отражающая влияние фактора Фj на Фi.

Неизвестные параметры k, b теоретической линии регрессии определяются путем минимизации функции квадратичных отклонений методом наименьших квадратов:
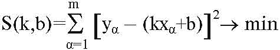
Тогда коэффициент регрессии вычисляется с помощью соотношений:
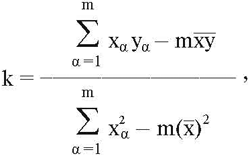
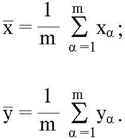
Сравнение традиционного и уточненного анализа прибыли
Рассмотрим упрощенную модель:
![]() (6)
(6)
где: TR – выручка; TC – общие затраты; P – цена товара; Q – объем продаж.
Проведем сравнительный анализ чувствительности прибыли к изменению факторов P и Q. Определим эластичность прибыли по: традиционной (вариант «а») и уточненной факторным моделям с учетом взаимного влияния факторов (вариант «б»).
ВАРИАНТ «А»
Коэффициент эластичности прибыли по цене ЕР и коэффициент ЕQ эластичности прибыли по объему продаж, вычисленные по формуле (2) в соответствии с традиционной факторной моделью, одинаковы:
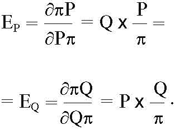
Они показывают, что при увеличении цены или объема продаж (при неизменных остальных показателях) прибыль π возрастает (рис. 2).
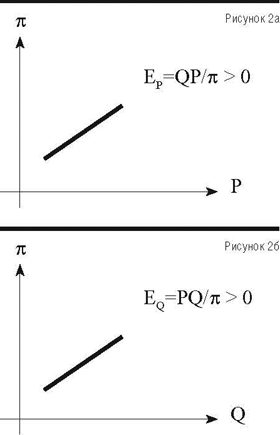
ВАРИАНТ «Б».
Анализ чувствительности прибыли при изменении сразу нескольких зависимых друг от друга показателей проводится с помощью уточненного факторного анализа. В качестве примера рассмотрим зависимость объема продаж от цены. Возможны 2 варианта: с ростом цены объем продаж падает (рис. 3а) или возрастает (рис. 3б).
В первом варианте имеет место классический закон спроса. Тогда снижение прибыли из-за уменьшения одного из факторов будет частично или полностью компенсироваться ростом второго фактора. Однако в любом случае уточненный коэффициент эластичности EIP будет меньше, чем коэффициент эластичности EP, так как производная δQ/δP<0 :
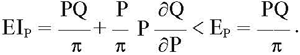
Какой из двух факторов (P или Q) даст больший вклад в изменение прибыли, можно выяснить по значению уточненного коэффициента эластичности. Возможны 3 случая.
1. Если EIP > 0, вклад фактора P в рост прибыли будет более значительным по сравнению с вкладом фактора Q – то есть увеличение цены дает прирост прибыли.
2. Если EIP < 0, увеличение цены неоправданно – падение объема продаж приводит к убыткам.
3. Если EIP = 0, увеличение цены и падение объема продаж нивелируют друг друга.
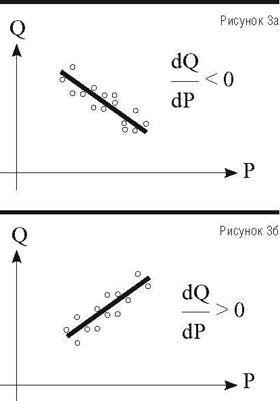
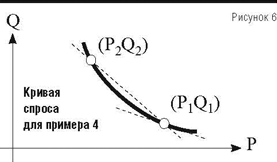
Второй вариант относится к так называемым товарам Веблена (товарам роскоши). Прибыль будет расти более быстрыми темпами сразу из-за двух положительно влияющих на нее факторов. Это подтверждается значением уточненного коэффициента эластичности. При вычислении по формуле (4) он принимает большее значение, чем рассчитанный по формуле (2), так как δQ/δP>0
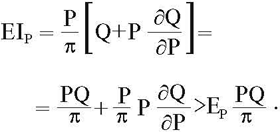
Примеры расчета прироста прибыли
Проанализируем работу компании в краткосрочном периоде. Представим общие затраты TC в выражении (6) в виде [3]:
![]() (7)
(7)
где: L – прямые затраты труда на единицу продукции (удельная трудоемкость); M – прямые затраты материалов на единицу продукции (удельная материалоемкость); IDC – косвенные затраты.
Таким образом, прибыль в данной модели – это функция 5 факторов:
![]() (8)
(8)
Коэффициенты эластичности, вычисленные по формуле (2), приведены в таблице 2.

Представим относительное изменение прибыли с использованием традиционной факторной модели:
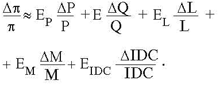 (9)
(9)
Будем считать, что объем продаж Q зависит от цены P. Остальные факторы являются независимыми и не влияют на другие. В этом случае прибыль будет представлять функцию уже 4 независимых факторов:
![]() (10)
(10)
Уточненные коэффициенты эластичности, вычисленные по формуле (4), приведены в таблице 3.

Относительное изменение прибыли с использованием уточненной факторной модели будет иметь вид:
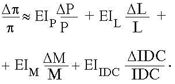 (11)
(11)
Определим условия, при которых относительное изменение прибыли компании в краткосрочном периоде, рассчитанное по традиционной и уточненной факторной модели, совпадают при любых приращениях факторов. Приравняв правые части соотношений (9) и (11), получим:
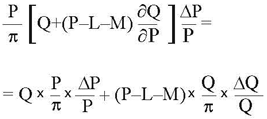
или (после несложных преобразований):
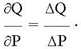 (12)
(12)
Равенство (12) при любых конечных приращениях факторов возможно только при условии линейной зависимости объема продаж от цены. Таким образом, традиционную факторную модель можно рассматривать как частный случай уточненной факторной модели при условии линейной зависимости между факторами.
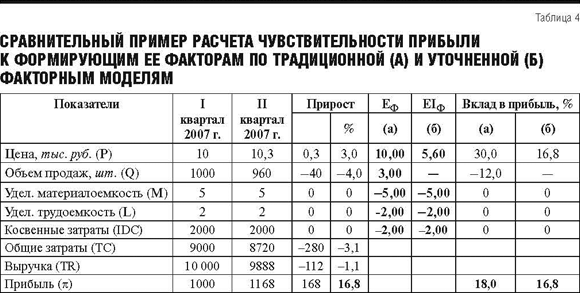
Пример 1. Рассмотрим классическую зависимость между объемом продаж и ценой товара. В таблице 4 приведены данные о прибыли компании за первые 2 квартала. Цена повысилась на 3%, что привело к снижению объема продаж на 4%. Прирост прибыли за II квартал составил 16,8%.
Сравним расчет чувствительности прибыли к составляющим ее факторам по традиционной (а) и уточненной (б) факторным моделям с учетом взаимного влияния факторов.
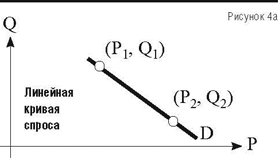
Расчет вклада факторов прибыли в общую прибыль по традиционной факторной модели дал прирост 18%. Отклонение в 1,2%, полученное благодаря использованию точечной эластичности, можно объяснить так. Использование традиционной факторной модели подразумевает линейную функцию спроса D (рис. 4а), которая соединяет 2 точки на траектории движения компании. На рисунке 4 точки 1 и 2, соответствующие I и II кварталам из таблицы 4, имеют координаты P1 = 10; Q1 = 1000 и P2= 10,3; Q2= 960. Кривая спроса описывается уравнением:
Q = –133,3 х P + 2333.
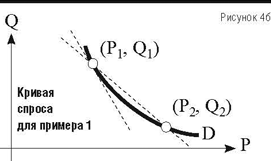
Использование уточненной факторной модели позволяет рассматривать нелинейную функцию спроса D (рис. 4б), которая соединяет те же 2 точки на траектории движения компании. Определим функцию спроса из предположения, что уточненная криволинейная функция спроса дает точное значение прироста прибыли 16,8%.
Поскольку прирост цены составил 0,3 тыс. руб., или 3%, а вклад в прибыль изменения цены дал 16,8%, то можно вычислить значение уточненного коэффициента эластичности прибыли по цене:
![]()
Используя выражение уточненного коэффициента эластичности EIP из таблицы 4, получаем уравнение для расчета производной от функции спроса по цене в точке 1:
 (13)
(13)
Функцию спроса представим в виде параболы, проходящей через точки 1 и 2 и имеющей в точке 1 производную, указанную выражением (13). Такая функция спроса показана на рисунке 4б. Тонкая сплошная прямая является касательной к кривой D в точке 1, а ее наклон определяется производной (13). Пунктиром для сравнения показана прямолинейная функция спроса, применяемая в традиционной факторной модели. Кривая спроса описывается уравнением:
![]()
Данное уравнение описывает кривую спроса на товары рассматриваемой компании в течение 2 кварталов ее работы (табл. 4).
Пример 2. Рассмотрим зависимость между объемом продаж и ценой товара при условии, что компания специализируется на продаже товаров роскоши. Предположим, что в значения показателей работы по сравнению с данными таблицы 4 внесено только одно изменение: объем продаж во II квартале составил Q2 = 1020. Таким образом, повышение цены на 3% сопровождалось повышением объема продаж на 2%. Прирост прибыли в процентах за II квартал по сравнению с I составил 36,6%.
Расчет вклада факторов прибыли в общую прибыль по традиционной факторной модели дал прирост 36%. Отклонение 0,6%, полученное вследствие использования точечной эластичности, показывает приемлемую точность данного метода. Использование традиционной факторной модели подразумевает линейную функцию спроса, которая на рисунке 5а показана пунктиром. Она описывается уравнением:
Q = 66,7 х P + 333,3.
По уточненной факторной модели рассмотрим нелинейную функцию спроса (кривая на рис. 5а), соединяющую те же 2 точки на траектории движения компании. Если предположить, что уточненная криволинейная функция спроса дает точное значение прироста прибыли 36,6%, то:
![]()
и уравнение функции спроса в виде полинома 2-й степени
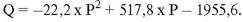
Пример 3. Рассмотрим зависимость между объемом продаж компании и ценой товара при условии, что на рынке появился сильный конкурент, играющий на понижение. Изменим значение показателей работы компании по сравнению с таблицей 4: цена во II квартале составила P2= 9,8. В этом случае снижение цены на 2% сопровождалось падением объема продаж на 4%, что привело к убыткам в 31,2%.
Расчет по традиционной факторной модели дал убыток в 32%. Линейная функция спроса (показана на рис. 5а пунктиром) описывается уравнением
Q = 200 х P – 1000.
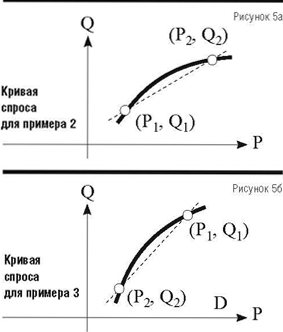
По уточненной факторной модели в предположении, что она дает точное значение убытка в 31,2%, определяем:
![]()
и уравнение функции спроса в виде полинома 2-й степени (кривая на рис. 5б)
Q = –66,7 х P2 + 1520 х P – 7533,3.
Рассмотренные примеры показывают, как в различных ситуациях смоделировать кривую спроса, с помощью которой можно прогнозировать дальнейшую траекторию движения компании.
1. Егерев И.А. Стоимость бизнеса: Искусство управления: учеб. пособие. – М., 2003. – 480 с.
2. Еленева Ю.Я., Волков А.Э., Волкова Г.Л. Факторный анализ стоимости предприятия с учетом оценки влияния нематериальных активов // Известия вузов. Машиностроение. 2006. № 3. С. 73–77.
3. Мицкевич А.А. Сбалансированная по прибыли система экономических показателей // Экономические стратегии. 2005. № 2. С. 88–93.